Difference between revisions of "Motivation for tangent space"
(Created page with "The isomorphism between tangents and derivations is surprising! As is the fact it is a linear map. However with calculus one is not far from that definition already. ==Motiva...") |
m |
||
| Line 41: | Line 41: | ||
These formulas are easily found from substitution. | These formulas are easily found from substitution. | ||
| − | {{ | + | ==Lines as seen in the polar coordinate plane== |
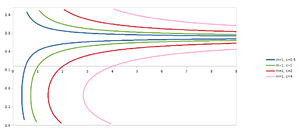
| + | [[Image:LinesInPolar.png|thumb|Some lines in polar coordinates, the y axis is the angle and the x radius<br/>all these lines have gradient 1 (the gradient would just affect where r tends off towards infinity, which happens at pi/4 here) and from left to right, c=0.5, 1, 2 and 4]] | ||
| + | |||
| + | (See diagram on right) - notice that there are some "iffy" parts with lines (as seen above) - there's a discontinuity at the asymptote! - let us see how it is drawn to understand why. | ||
| + | |||
| + | ===Drawing the line y=x+1=== | ||
| + | Using the equation above we see: | ||
| + | * <math>r=|c|\sqrt{\frac{(m^2+1)}{(\tan(\theta)-m)^2}+\frac{2m}{\tan(\theta)-m}+1}</math> becomes | ||
| + | * <math>r=\sqrt{\frac{2}{(\tan(\theta)-1)^2}+\frac{2}{\tan(\theta)-1} + 1}</math> - this isn't that useful though. | ||
| + | |||
| + | Consider drawing the graph, the logic goes as follows: | ||
| + | * {{M|1=\theta=0}} - well where can {{M|r}} actually be now? Undefined? If you graph the above, {{M|1=r=1}} | ||
| + | * As {{M|\theta}} increases, we keep drawing {{M|1=y=x-1}} - it grows faster and faster as we get near {{M|1=\theta=\tfrac{\pi}{4} }} | ||
| + | * {{M|\theta=\tfrac{\pi}{4} }} - {{M|r}} is undefined! | ||
| + | * {{M|\theta}} increases further - we now start to come back down, and we draw {{M|1=y=x+1}}, this keeps being drawn until: | ||
| + | * {{M|1=\theta=\tfrac{3\pi}{4} }} - we become undefined for {{M|r}} again | ||
| + | * {{M|\theta}} increases further - we draw more of {{M|1=y=x-1}}, until we meet {{M|\theta=0}} | ||
| + | |||
| + | |||
| + | ==Tangents== | ||
| + | Let us go from tangents in {{M|(x,y)}} to tangents in {{M|(r,\theta)}} | ||
| + | |||
| + | |||
| + | Using the notation of [[Motivation for smooth manifolds#Our charts|the charts for the smooth manifold of (upper quadrant) of the plane]] we can use the transition map: | ||
| + | * <math>(\beta\circ\alpha^{-1}):\mathbb{R}^2_++\rightarrow\mathbb{R}_+\times(0,\tfrac{\pi}{2})</math> | ||
| + | * <math>(\beta\circ\alpha^{-1}):(x,y)\mapsto\left(\sqrt{x^2+y^2},\arctan\left(\frac{y}{x}\right)\right)</math> | ||
| + | to go from the plane in terms of {{M|(x,y)}} to the {{M|(r,\theta)}} "chart" of the plane. | ||
| + | |||
| + | |||
| + | Let us compute the [[Jacobian]] of this map (at the point {{M|(x,y)}}: | ||
| + | : <math>\text{Jac}(\beta\circ\alpha^{-1})=\begin{pmatrix} | ||
| + | \frac{\partial r}{\partial x} & \frac{\partial r}{\partial y} \\ | ||
| + | \frac{\partial \theta}{\partial x} & \frac{\partial \theta}{\partial y} | ||
| + | \end{pmatrix}=\begin{pmatrix} | ||
| + | \frac{x}{\sqrt{x^2+y^2}} & \frac{y}{\sqrt{x^2+y^2}} \\ | ||
| + | \frac{-y}{x^2+y^2} & \frac{x}{x^2+y^2} | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | ===Notes about dimensions=== | ||
| + | Unit wise: | ||
| + | |||
| + | <math>\begin{pmatrix} | ||
| + | \frac{\delta r}{\delta x} & \frac{\delta r}{\delta y} \\ | ||
| + | \frac{\delta \theta}{\delta x} & \frac{\delta \theta}{\delta y} | ||
| + | \end{pmatrix}\times\begin{pmatrix} | ||
| + | \delta x \\ \delta y | ||
| + | \end{pmatrix}= | ||
| + | \begin{pmatrix} | ||
| + | \frac{\delta r}{\delta x}\delta x + \frac{\delta r}{\delta y}\delta y \\ | ||
| + | \frac{\delta \theta}{\delta x}\delta x + \frac{\delta \theta}{\delta y}\delta y | ||
| + | \end{pmatrix}=\begin{pmatrix} | ||
| + | \delta r \\ \delta \theta | ||
| + | \end{pmatrix}</math> | ||
| + | ===Calculating tangents=== | ||
| + | Where {{M|(u,v)}} is a column vector representing a tangent (in the sense of direction) in the {{M|(x,y)}} sense of the manifold we can compute the following: | ||
| + | |||
| + | : <math>\begin{pmatrix} | ||
| + | \frac{x}{\sqrt{x^2+y^2}} & \frac{y}{\sqrt{x^2+y^2}} \\ | ||
| + | \frac{-y}{x^2+y^2} & \frac{x}{x^2+y^2} | ||
| + | \end{pmatrix}\times\begin{pmatrix} | ||
| + | u \\ | ||
| + | v | ||
| + | \end{pmatrix}=\begin{pmatrix} | ||
| + | \frac{x}{\sqrt{x^2+y^2}}u+\frac{y}{\sqrt{x^2+y^2}}v \\ | ||
| + | \frac{-y}{x^2+y^2}u+\frac{x}{x^2+y^2}v | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | Notice that so far we have not mentioned any sort of "function", and this is linear! (at a point anyway) | ||
| + | |||
| + | ====Specific tangent==== | ||
| + | Take {{M|1=y=x+1}}, at {{M|1=x=1}} we see {{M|1=\frac{dy}{dx}=1}}, that is to say the tangent at {{M|1=p=(1,2)}} is {{M|(1,1)_p}} | ||
| + | |||
| + | : <math>\text{Jac}(\beta\circ\alpha^{-1})\begin{pmatrix} | ||
| + | 1 \\ 1 \end{pmatrix} = \begin{pmatrix} | ||
| + | \frac{3\sqrt{5}}{5} \\ \frac{-1}{5} | ||
| + | \end{pmatrix}</math> (using graphical calculator) | ||
| + | |||
| + | From this we see: | ||
| + | : <math>\frac{dr}{d\theta}=\frac{\frac{3\sqrt{5}}{5}}{\frac{-1}{5}}=-3\sqrt{5}\approx-6.708\text{ (4sf)}</math> | ||
| + | |||
| + | |||
| + | Using my graphical calculator I found: | ||
| + | |||
| + | : <math>\left.\frac{d}{dt}\left[ | ||
| + | |c|\sqrt{\frac{(m^2+1)}{(\tan(t)-m)^2}+\frac{2m}{\tan(t)-m}+1} | ||
| + | \right]\right|_{t=\arctan(\frac{y}{x})}\approx -6.708\text{ (4sf)}</math> | ||
| + | : where | ||
| + | :* {{M|1=m=1}} | ||
| + | :* {{M|1=c=1}} | ||
| + | :* {{M|1=(x,y)=p}} | ||
| + | |||
| + | {{Todo| get back to tangent space}} | ||
==References== | ==References== | ||
Latest revision as of 00:18, 11 April 2015
The isomorphism between tangents and derivations is surprising! As is the fact it is a linear map. However with calculus one is not far from that definition already.
Contents
Motivating example
Let us take (informally, because cases where [ilmath]\theta=\tfrac{\pi}{2}[/ilmath] and [ilmath]r=0[/ilmath] must be treated carefully) the manifold of the plane. The reader should be familiar with polar coordinates (giving things as an angle and a distance from the origin, rather than [ilmath]x[/ilmath] and [ilmath]y[/ilmath])
We will have two ways of looking at points, as [ilmath](x,y)[/ilmath] - traditionally, and [ilmath](r,\theta)[/ilmath] where:
- [ilmath](r,\theta)\mapsto(r\cos(\theta),r\sin(\theta))[/ilmath]
- [ilmath](x,y)\mapsto\left(\sqrt{x^2+y^2},\arctan(\frac{y}{x})\right)[/ilmath]
The line
Take the line [ilmath]y=mx+c[/ilmath], where [ilmath]m[/ilmath] is the gradient and [ilmath]c[/ilmath] is the intercept with the y axis, writing this we see the line can be given as:
| Form | First coord | Second coord |
|---|---|---|
| [ilmath]x,y[/ilmath] | [ilmath]x=t[/ilmath] | [ilmath]y=mt+c[/ilmath] |
| [ilmath]r,\theta[/ilmath] | [ilmath]r=\sqrt{t^2(m^2+1)+2mct+c^2}[/ilmath] | [ilmath]\theta=\arctan\left(m+\frac{c}{t}\right)[/ilmath] |
| Pure forms | ||
| Form | map | |
| Cartesian | [ilmath]y=mx+c[/ilmath] | |
| Polar[1] | [math]r=|c|\sqrt{\frac{(m^2+1)}{(\tan(\theta)-m)^2}+\frac{2m}{\tan(\theta)-m}+1}[/math] | |
These formulas are easily found from substitution.
Lines as seen in the polar coordinate plane
(See diagram on right) - notice that there are some "iffy" parts with lines (as seen above) - there's a discontinuity at the asymptote! - let us see how it is drawn to understand why.
Drawing the line y=x+1
Using the equation above we see:
- [math]r=|c|\sqrt{\frac{(m^2+1)}{(\tan(\theta)-m)^2}+\frac{2m}{\tan(\theta)-m}+1}[/math] becomes
- [math]r=\sqrt{\frac{2}{(\tan(\theta)-1)^2}+\frac{2}{\tan(\theta)-1} + 1}[/math] - this isn't that useful though.
Consider drawing the graph, the logic goes as follows:
- [ilmath]\theta=0[/ilmath] - well where can [ilmath]r[/ilmath] actually be now? Undefined? If you graph the above, [ilmath]r=1[/ilmath]
- As [ilmath]\theta[/ilmath] increases, we keep drawing [ilmath]y=x-1[/ilmath] - it grows faster and faster as we get near [ilmath]\theta=\tfrac{\pi}{4}[/ilmath]
- - [ilmath]r[/ilmath] is undefined!
- [ilmath]\theta[/ilmath] increases further - we now start to come back down, and we draw [ilmath]y=x+1[/ilmath], this keeps being drawn until:
- [ilmath]\theta=\tfrac{3\pi}{4}[/ilmath] - we become undefined for [ilmath]r[/ilmath] again
- [ilmath]\theta[/ilmath] increases further - we draw more of [ilmath]y=x-1[/ilmath], until we meet
Tangents
Let us go from tangents in [ilmath](x,y)[/ilmath] to tangents in [ilmath](r,\theta)[/ilmath]
Using the notation of the charts for the smooth manifold of (upper quadrant) of the plane we can use the transition map:
- [math](\beta\circ\alpha^{-1}):\mathbb{R}^2_++\rightarrow\mathbb{R}_+\times(0,\tfrac{\pi}{2})[/math]
- [math](\beta\circ\alpha^{-1}):(x,y)\mapsto\left(\sqrt{x^2+y^2},\arctan\left(\frac{y}{x}\right)\right)[/math]
to go from the plane in terms of [ilmath](x,y)[/ilmath] to the [ilmath](r,\theta)[/ilmath] "chart" of the plane.
Let us compute the Jacobian of this map (at the point [ilmath](x,y)[/ilmath]:
- [math]\text{Jac}(\beta\circ\alpha^{-1})=\begin{pmatrix} \frac{\partial r}{\partial x} & \frac{\partial r}{\partial y} \\ \frac{\partial \theta}{\partial x} & \frac{\partial \theta}{\partial y} \end{pmatrix}=\begin{pmatrix} \frac{x}{\sqrt{x^2+y^2}} & \frac{y}{\sqrt{x^2+y^2}} \\ \frac{-y}{x^2+y^2} & \frac{x}{x^2+y^2} \end{pmatrix}[/math]
Notes about dimensions
Unit wise:
[math]\begin{pmatrix} \frac{\delta r}{\delta x} & \frac{\delta r}{\delta y} \\ \frac{\delta \theta}{\delta x} & \frac{\delta \theta}{\delta y} \end{pmatrix}\times\begin{pmatrix} \delta x \\ \delta y \end{pmatrix}= \begin{pmatrix} \frac{\delta r}{\delta x}\delta x + \frac{\delta r}{\delta y}\delta y \\ \frac{\delta \theta}{\delta x}\delta x + \frac{\delta \theta}{\delta y}\delta y \end{pmatrix}=\begin{pmatrix} \delta r \\ \delta \theta \end{pmatrix}[/math]
Calculating tangents
Where [ilmath](u,v)[/ilmath] is a column vector representing a tangent (in the sense of direction) in the [ilmath](x,y)[/ilmath] sense of the manifold we can compute the following:
- [math]\begin{pmatrix} \frac{x}{\sqrt{x^2+y^2}} & \frac{y}{\sqrt{x^2+y^2}} \\ \frac{-y}{x^2+y^2} & \frac{x}{x^2+y^2} \end{pmatrix}\times\begin{pmatrix} u \\ v \end{pmatrix}=\begin{pmatrix} \frac{x}{\sqrt{x^2+y^2}}u+\frac{y}{\sqrt{x^2+y^2}}v \\ \frac{-y}{x^2+y^2}u+\frac{x}{x^2+y^2}v \end{pmatrix}[/math]
Notice that so far we have not mentioned any sort of "function", and this is linear! (at a point anyway)
Specific tangent
Take [ilmath]y=x+1[/ilmath], at [ilmath]x=1[/ilmath] we see [ilmath]\frac{dy}{dx}=1[/ilmath], that is to say the tangent at [ilmath]p=(1,2)[/ilmath] is [ilmath](1,1)_p[/ilmath]
- [math]\text{Jac}(\beta\circ\alpha^{-1})\begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{3\sqrt{5}}{5} \\ \frac{-1}{5} \end{pmatrix}[/math] (using graphical calculator)
From this we see:
- [math]\frac{dr}{d\theta}=\frac{\frac{3\sqrt{5}}{5}}{\frac{-1}{5}}=-3\sqrt{5}\approx-6.708\text{ (4sf)}[/math]
Using my graphical calculator I found:
- [math]\left.\frac{d}{dt}\left[ |c|\sqrt{\frac{(m^2+1)}{(\tan(t)-m)^2}+\frac{2m}{\tan(t)-m}+1} \right]\right|_{t=\arctan(\frac{y}{x})}\approx -6.708\text{ (4sf)}[/math]
- where
- [ilmath]m=1[/ilmath]
- [ilmath]c=1[/ilmath]
- [ilmath](x,y)=p[/ilmath]
TODO: get back to tangent space