Notes:Grid iteration
See Modulo operator for a definition of [ilmath]\text{Mod}(a,b)[/ilmath]
2D grid
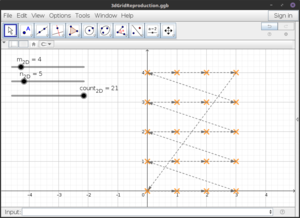

- [math]\text{Mix}_x(k,m,n):\eq \text{Floor}\left(\text{Mod}\big(\text{Mod}(k,mn),m\big)\right)[/math]
- [math]\text{Mix}_y(k,m,n):\eq \frac{\text{Mod}(k,mn)-\text{Mod}\big(\text{Mod}(k,mn),m\big)}{m} [/math]
Then
- Points of the form:
- [math]\big(\text{Mix}_x(k,m,n),\text{Mix}_y(k,m,n)\big)[/math] span an [ilmath]m\times n[/ilmath] grid, for [ilmath]k[/ilmath] from [ilmath]0[/ilmath] to [ilmath]mn-1[/ilmath]
Notice that these coordinates return to the start for [ilmath]\text{count}\eq 21[/ilmath] or [ilmath]k\eq 20[/ilmath], this is critical to allowing this to be used in higher dimensions.
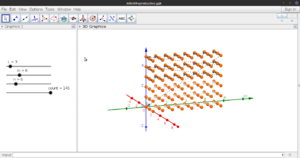
3D grid

Suppose we have an [ilmath]\ell\times m\times n[/ilmath] grid, we can build this using [ilmath]\text{Mix}_x[/ilmath] and [ilmath]\text{Mix}_y[/ilmath]:
- for [ilmath]k\in\mathbb{N}_0[/ilmath] with [ilmath]0\le k\le \ell\times m\times n-1[/ilmath]
- [ilmath]x[/ilmath]-coordinate: [ilmath]\text{Mix}_x(k,\ell,m\times n) [/ilmath]
- [ilmath]y[/ilmath]-coordinate: [ilmath]\text{Mix}_x\big(\text{Mix}_y(k,\ell,m\times n),m,n\big)[/ilmath]
- [ilmath]z[/ilmath]-coordinate: [ilmath]\text{Mix}_y\big(\text{Mix}_y(k,\ell,m\times n),m,n\big)[/ilmath]
In the picture on the right we show a [ilmath]3\times 8\times 6[/ilmath] example, notice that these multiplied give [ilmath]144[/ilmath] ([ilmath]k\eq 144-1\eq 143[/ilmath]), we do [ilmath]145[/ilmath] ([ilmath]k\eq 144[/ilmath]) instead, this gives the diagonal returning back to the 1st point, and is the key property in allowing this concept to extend to higher dimensions (returning to the start, where we would increase the 4th dimension to create a distinct point, if we did so here)
Generalisation
TODO: Explain method, generalise to arbitrary dimensions