Motivation for tangent space

The isomorphism between tangents and derivations is surprising! As is the fact it is a linear map. However with calculus one is not far from that definition already.

Motivating example

Let us take (informally, because cases where $\theta=\tfrac{\pi}{2}$ and $r=0$ must be treated carefully) the manifold of the plane. The reader should be familiar with polar coordinates (giving things as an angle and a distance from the origin, rather than $x$ and $y$)

We will have two ways of looking at points, as $(x,y)$ - traditionally, and $(r,\theta)$ where:

• $(r,\theta)\mapsto(r\cos(\theta),r\sin(\theta))$
• $(x,y)\mapsto\left(\sqrt{x^2+y^2},\arctan(\frac{y}{x})\right)$

The line

Take the line $y=mx+c$, where $m$ is the gradient and $c$ is the intercept with the y axis, writing this we see the line can be given as:

Form	First coord	Second coord
$x,y$	$x=t$	$y=mt+c$
$r,\theta$	$r=\sqrt{t^2(m^2+1)+2mct+c^2}$	$\theta=\arctan\left(m+\frac{c}{t}\right)$
Pure forms
Form	map
Cartesian	$y=mx+c$
Polar	$$r=|c|\sqrt{\frac{(m^2+1)}{(\tan(\theta)-m)^2}+\frac{2m}{\tan(\theta)-m}+1}$$

These formulas are easily found from substitution.

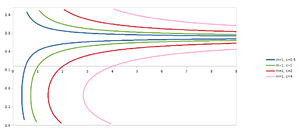
Lines as seen in the polar coordinate plane

Some lines in polar coordinates, the y axis is the angle and the x radius
all these lines have gradient 1 (the gradient would just affect where r tends off towards infinity, which happens at pi/4 here) and from left to right, c=0.5, 1, 2 and 4

(See diagram on right) - notice that there are some "iffy" parts with lines (as seen above) - there's a discontinuity at the asymptote! - let us see how it is drawn to understand why.

Drawing the line y=x+1

Using the equation above we see:

• $$r=|c|\sqrt{\frac{(m^2+1)}{(\tan(\theta)-m)^2}+\frac{2m}{\tan(\theta)-m}+1}$$ becomes
• $$r=\sqrt{\frac{2}{(\tan(\theta)-1)^2}+\frac{2}{\tan(\theta)-1} + 1}$$ - this isn't that useful though.

Consider drawing the graph, the logic goes as follows:

• $\theta=0$ - well where can $r$ actually be now? Undefined? If you graph the above, $r=1$
• As $\theta$ increases, we keep drawing $y=x-1$ - it grows faster and faster as we get near $\theta=\tfrac{\pi}{4}$
• - $r$ is undefined!
• $\theta$ increases further - we now start to come back down, and we draw $y=x+1$, this keeps being drawn until:
• $\theta=\tfrac{3\pi}{4}$ - we become undefined for $r$ again
• $\theta$ increases further - we draw more of $y=x-1$, until we meet

Tangents

Let us go from tangents in $(x,y)$ to tangents in $(r,\theta)$

Using the notation of the charts for the smooth manifold of (upper quadrant) of the plane we can use the transition map:

• $$(\beta\circ\alpha^{-1}):\mathbb{R}^2_++\rightarrow\mathbb{R}_+\times(0,\tfrac{\pi}{2})$$
• $$(\beta\circ\alpha^{-1}):(x,y)\mapsto\left(\sqrt{x^2+y^2},\arctan\left(\frac{y}{x}\right)\right)$$

to go from the plane in terms of $(x,y)$ to the $(r,\theta)$ "chart" of the plane.

Let us compute the Jacobian of this map (at the point $(x,y)$:

$$\text{Jac}(\beta\circ\alpha^{-1})=\begin{pmatrix} \frac{\partial r}{\partial x} & \frac{\partial r}{\partial y} \\ \frac{\partial \theta}{\partial x} & \frac{\partial \theta}{\partial y} \end{pmatrix}=\begin{pmatrix} \frac{x}{\sqrt{x^2+y^2}} & \frac{y}{\sqrt{x^2+y^2}} \\ \frac{-y}{x^2+y^2} & \frac{x}{x^2+y^2} \end{pmatrix}$$

Notes about dimensions

Unit wise:

$$\begin{pmatrix} \frac{\delta r}{\delta x} & \frac{\delta r}{\delta y} \\ \frac{\delta \theta}{\delta x} & \frac{\delta \theta}{\delta y} \end{pmatrix}\times\begin{pmatrix} \delta x \\ \delta y \end{pmatrix}= \begin{pmatrix} \frac{\delta r}{\delta x}\delta x + \frac{\delta r}{\delta y}\delta y \\ \frac{\delta \theta}{\delta x}\delta x + \frac{\delta \theta}{\delta y}\delta y \end{pmatrix}=\begin{pmatrix} \delta r \\ \delta \theta \end{pmatrix}$$

Calculating tangents

Where $(u,v)$ is a column vector representing a tangent (in the sense of direction) in the $(x,y)$ sense of the manifold we can compute the following:

$$\begin{pmatrix} \frac{x}{\sqrt{x^2+y^2}} & \frac{y}{\sqrt{x^2+y^2}} \\ \frac{-y}{x^2+y^2} & \frac{x}{x^2+y^2} \end{pmatrix}\times\begin{pmatrix} u \\ v \end{pmatrix}=\begin{pmatrix} \frac{x}{\sqrt{x^2+y^2}}u+\frac{y}{\sqrt{x^2+y^2}}v \\ \frac{-y}{x^2+y^2}u+\frac{x}{x^2+y^2}v \end{pmatrix}$$

Notice that so far we have not mentioned any sort of "function", and this is linear! (at a point anyway)

Specific tangent

Take $y=x+1$, at $x=1$ we see $\frac{dy}{dx}=1$, that is to say the tangent at $p=(1,2)$ is $(1,1)_p$

$$\text{Jac}(\beta\circ\alpha^{-1})\begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{3\sqrt{5}}{5} \\ \frac{-1}{5} \end{pmatrix}$$ (using graphical calculator)

From this we see:

$$\frac{dr}{d\theta}=\frac{\frac{3\sqrt{5}}{5}}{\frac{-1}{5}}=-3\sqrt{5}\approx-6.708\text{ (4sf)}$$

Using my graphical calculator I found:

$$\left.\frac{d}{dt}\left[ |c|\sqrt{\frac{(m^2+1)}{(\tan(t)-m)^2}+\frac{2m}{\tan(t)-m}+1} \right]\right|_{t=\arctan(\frac{y}{x})}\approx -6.708\text{ (4sf)}$$

where

• $m=1$
• $c=1$
• $(x,y)=p$

---

TODO: get back to tangent space

---